笔者对球类运动物理学的兴趣是从一个具体问题开始的,即足球守门员如果用很大的力气,在同样的角度和初速度下踢球,哪个会飞得更远,表面光滑的球还是表面光滑的球?表面粗糙的球?笔者和大多数被问到的人一样,基于直觉,认为光滑的球在飞行时的空气阻力更小,所以选择了前者,但遗憾的是答案是错误的。有几个人觉得这个问题一定有玄机,所以选择了后者,但我也说不出原因。为了寻找问题的答案,笔者在阅读相关书籍和文献的过程中,逐渐涉足了其他球类运动。本文以球的飞行和滚动为中心,选取了阅读中得到的几个片段和读物。分享给大家,文章将从上述问题开始。

图1 足球运动员大力踢球
1 表面光滑的球和表面粗糙的球哪个飞得更远?
关于球飞行动力学的研究起步较早,在高尔夫球方面做的工作较多。早在1910年,著名物理学家JJ汤姆森就发表了这方面的研究论文,随后的研究工作导致采用了在球表面布满小凹坑的设计,以使球飞得更远。事实上,表面光滑的球被职业球员击打后的飞行距离大约只有一半,球完全凹陷。回到我们经常接触的足球,根据比赛规则,球的外壳必须由皮革片制成,并通过预先穿好螺纹的针孔缝合在一起。针孔总数约为2000个,缝合槽深度约为1-2毫米。 ,球表面的这些接缝凹槽对球的飞行也有重要的影响。守门员用力踢球,把球踢进对方半场是常有的事,但如果用光滑的球,就没有缝线槽的功劳了。恐怕不容易做到,粗糙表面之所以会降低空气阻力,涉及到“边界层”的概念。
对于空气、水和油等实际粘性流体,其动态行为由纳维-斯托克斯方程(简称NS方程)描述。对于具体问题,给出相应的初始条件和边条件。原则上是可以得到答案的。由于这是一组非线性二阶偏微分方程,且具体问题的附带条件往往非常复杂,因此只能在少数具体情况下才能求解。一个常见的例子是使用沉降球来测量油的粘度系数 η,即雷诺数 Rer,如图 7 所示。如果 x 选择适当,沉降球从一开始就可以以滚动形式运动。击中它还有两个作用:一方面,使D点向右移动;另一方面,使D点向右移动。另一方面,由于力没有经过球中心,导致球顺时针旋转,导致D点向左移动。球不滑动而仅旋转的条件是,在击球的瞬间,D点与台面之间没有初始相对运动(因此这里不涉及摩擦力)。这就需要一个合适的x值来使得D点的瞬时行为就像一个静止的旋转轴。从抵消上述两个影响出发,以D点静止为条件,可得
x=(7/5)r=(7/10)d,
其中,d=2r为球的直径。击球点应高于球台并等于球直径的7/10。
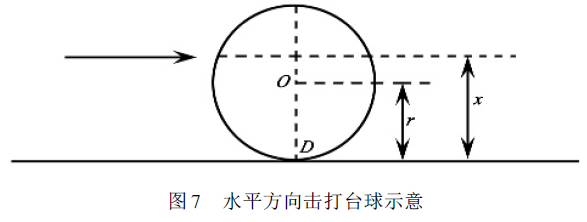
图7 水平方向击球示意图
英式斯诺克球的直径约为5厘米,滑动时能量损失明显减少,速度的下降也相应减弱。出于同样的原因,这个位置也是运动员正常击球时经常选择的击球点。
保龄球道的 7 个谜团

与台球相比,保龄球在球道内运动的分析更为复杂。首先,车道的摩擦系数不能简单地视为常数;其次,虽然有指孔的保龄球的重量和直径受到规则的限制,但并不要求球完全均匀、对称。事实上,由树脂材料制成的保龄球中填充有不同形状的配重块,导致球穿过球中心且具有不同方向的轴线的回转半径不同,以及球中心和球的位置不同。质心。巧合的是,结果是在讨论球的旋转时,转动惯量张量不能对角化。对于制作精良、质量上乘的球来说,这种差异被限制在很小的范围内,例如,任意两轴的回转半径之差不能大于0.2厘米,球中心与球体之间的距离不能大于0.2cm。质心必须控制在小于或等于1毫米。数值模拟计算表明,这一微小的差异仍然对球的轨迹产生重大影响。
打保龄球的人都知道,投出的球应该是曲线球或左曲球。右手选手投出的球应在 1 号瓶(第一个瓶)和 3 号瓶之间切成一定角度,这样很容易导致瓶倾斜并侧向掉落,而击中的概率是最高的。除了投出的球必须具有一定的初速度和侧向旋转外,模拟计算表明沿球道摩擦系数的变化是最重要的因素。
保龄球道宽 42 英寸,相当于 1.06 m。从罚球线到旗杆区中心的 1 号旗杆的长度为 60 英尺,相当于 18.28 m。它由39-42块木板条组成。球员投球的走道和球道的前20英尺以及球道的旗杆设置区均由枫木制成。枫木非常坚硬,可以承受16磅重的球对其表面产生的近130公斤/厘米2的持续冲击力。球道中段由硬度相对较低的松木制成。松木的质感比较好,摩擦系数也会比较高。但实际上,决定球道摩擦系数变化的关键因素是球道表面的注油以及不同的注油布置。它可以改变游戏的难度;比赛过程中,还应注意球带出的油污引起的球道状况的变化。
涂油区一般如图8中灰色区域所示,宽度为球道宽度的4/5,长度为距罚球线40英尺。根据规则,球道的摩擦系数不能超过0.39。有薄油层的区域,摩擦系数的典型值为0.04,无油区域的摩擦系数一般不超过0.20。球场的初始速度和旋转度数取中级球员的值,分别为8 m/s和30。 ran/s(相当于每秒 4.77 转)。图8示出了保龄球在上述情况下,当球处于两种差异较大的状态时(如图(a)和(b)所示)的运动轨迹。仿真计算的结果,图8中的箭头显示了球的角速度的方向。
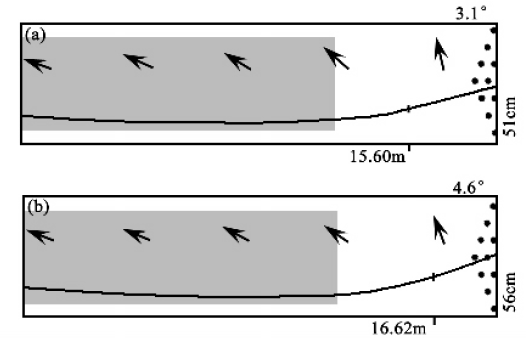
图8 保龄球运动轨迹仿真计算结果 (a) 转动惯量为标量,回转半径取低值6.2 cm,球的质心与球中心重合; (b) 转动惯量是张量,绕三个主轴的回转半径取高值分别为6.9 cm、7.1 cm、7.1 cm。质心与球中心之间的距离为0.7毫米。
从图8所示的结果可以看出,无论球的质心是否与球的中心重合,以及转动惯量是否为张量,都对球的运动轨迹产生影响,并使得图8(a)和8(b)中的球巷道细节有所不同,但最重要的因素是薄层油引起的球道摩擦系数的变化。图中的球路可以理解为:在注油区域,球路影响很小。球的轨迹一般是一条直线。离开注油区,球道的摩擦系数突然增大。当球接近旗杆区域时,摩擦力会导致球的路径发生偏转。最后,以理想的 3-5° 斜角进行切割。如果整个球道都涂了油,则摩擦系数恒定且较低,球路会很直,但在接近旗杆区时不会有足够的偏转;反之,如果不涂油,摩擦系数就高,球道就会偏斜,但球会因滚动而偏斜。太早的话将很难以理想的角度击球。
8 结论
首先,从中学物理和基础大学物理教学的角度来看,球类运动物理对于提高学生的学习兴趣、加深对问题的理解非常有帮助。篮球运动员在奔跑时运球,除非他们想改变速度和方向,否则只是垂直向下投篮。跑步时射击与站立射击不同。投篮的瞄准点必须根据跑动的速度和方向来调整,因为当球离开手时,它就承载着球员跑动的速度。 。当跑动的球员感觉到球在垂直向下或向上运动时,在场外观众看来,球实际上是在斜向前运动。在力学教学中,学生学习运动坐标系和惯性原理等概念的介绍。这些球场上的经历是一个很好的起点。本文讨论的一些与球的运动和碰撞有关的问题也将成为基础物理教学中学生非常感兴趣的练习或例子。
其次,从运动员和教练的角度来看,了解球类运动背后的物理原理重要吗?本文讨论了射击的准确性。投篮时,球的出手角度会随着球员与篮筐之间的距离而变化。出手角度确定后,篮球从篮筐中心进入篮筐,刚好触及框架边缘。根据数值计算得出,出球时的球速差异小于1%,初速度值的容差实际上很小。然而我们注意到,通过刻苦的练习和探索,运动员可以拥有非常好的运动技能。凭借运动和肌肉记忆,职业球员无需干扰或练习即可投篮 70% 或更高。作为物理学家,我们可以说的是,一方面,从优秀运动员的投篮、速度、技术等角度,可以检验和修正理论分析中使用的物理模型;另一方面,运动员了解相关原理后,在实践中会更加自觉,缩短探索的过程。
三是提高体育水平需要创新。以乒乓球为例。据统计,从20世纪50年代到1980年代初,中国乒乓球队处于领先地位时,共有29项被世界认可的技术创新,其中22项来自中国,占总数的75.9% 。但从1988年到1999年,中国仅拥有七项公认的创新技术之一,所占份额下降到14.3%。现阶段中国乒乓球队在重要比赛中失利,留下遗憾。持续的。尽管这些技术创新大多是运动员和教练员在实践中探索的,但显然仍需要从理论上进行解释和完善。当然,研究人员也需要提出建议并开发新技术。在这两方面,物理研究发挥着重要作用。
最后,对于球类运动物理学的研究,总体来说,美国和欧洲国家开展的研究较多,主要集中在本国流行的运动项目上,如高尔夫、网球、垒球、足球和台球等。有系统、深入的文章,也出版了一些相关书籍。从发表的文章和书籍来看,物理学家的积极参与应该对提高研究水平有很大帮助,例如英国物理学会J.出版的《足球的科学》一书的作者J.韦森的研究生涯始于实验原子和等离子体物理学,然后转向理论物理学,退休前踢足球。 RK Adair,美国出版的《棒球物理学》一书的作者,是耶鲁大学研究基本粒子的理论物理学教授,美国国家科学院院士,当然也是一名垒球迷。相对而言,国内的研究是逊色的,特别是在深度上,尤其是我们的优势项目,比如乒乓球。相关研究工作只能靠我们自己,需要从理论和实验方面加强。作者撰写本文的主要目的是引起读者的关注,希望国内物理学家能够参与球类运动和其他运动项目的物理学研究,为提高我国的体育水平做出贡献。
致谢感谢首都体育学院严守富教授对本文初稿的审阅并提出了很好的修改建议;并感谢贾秋萍女士在材料等方面的帮助。
本文选自《物理》2008年第7期
十大热门文章
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
结尾
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容, 请联系本站,一经查实,本站将立刻删除。如若转载,请注明出处:http://51shangxian.com/html/tiyuwenda/13172.html



